We represent the world to children as mostly known and rather dull. The opposite is the case: we are surrounded by mystery, and what we know is fascinating. - Kieran Egan
I came across Kieran Egan through a book review a friend shared with me. The way he crystalizes a problem that I could never quite put into words shed clarity on today's curriculum landscape. It also resonated with my earlier exposure to Paul Lockhart's A Mathematician's Lament
, which lands a much more extreme rebuke of modern mathematics education. For example, his description of a Pre-Calculus
course
:
PRE-CALCULUS. A senseless bouillabaisse of disconnected topics. Mostly a half-baked attempt to introduce late-nineteenth-century analytic methods into settings where they are neither necessary nor helpful. Technical definitions of limits and continuity are presented in order to obscure the intuitively clear notion of smooth change. As the name suggests, this course prepares the student for Calculus, where the final phase in the systematic obfuscation of any natural ideas related to shape and motion will be completed.
These are two people (of many) who have pointed to flaws in the current state of math educational. Lockhart has two books that offer a model for Primary Schools. As a secondary and post-secondary educator, I have not seen enrichment models that seek to go back and heal the trauma caused by a system that emphasizes and rewards algorithmic thinking and often penalizes creativity, ​ingenuity, or deep understanding.
Students will always adapt to the priorities of the curriculum presented to them. This means they do their best to learn the algorithms presented in class and ​dutifully practice them with similar problems at home. All of this is in preparation for a test, which also contains similar problems. The standard curriculum is a wonderful model for training a workforce to follow instructions without questioning it - but not a faithful presentation of the true purpose of learning mathematics!
Seminars at Diverging Mathematics revisit topics students have already learned - but with a twist. Starting with a common foundation, we change the rules a little and get plunged into a world where we need to go back and question everything. The worlds look similar and many of the usual tools are still effective - but questions will quickly pull students in directions that diverge from the common path.
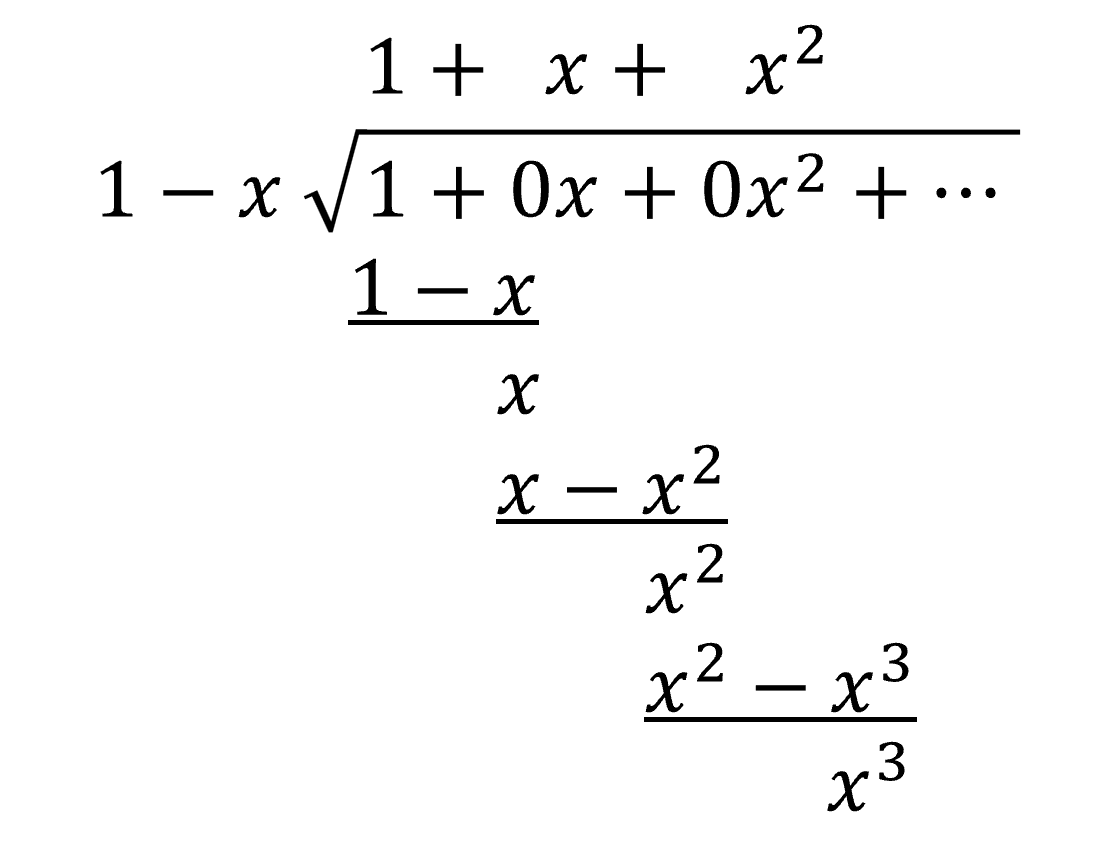
What does this quotient tell us about the original function? Consider values of \(x \approx 0\).
Looking at the pattern when working through the long division, it may look familiar. Think \(10/9 = 1.111... = 1.\bar{1}\) ). But if we continue forever, what would it even mean to have infinitely many terms?
Try plugging in \(x = 1/10\). Does this check out?
Ok, so this seem to work, but it is still strange. What happens for other values of \(x\)?! Things get weird if \(x=-1\) or \(x=-2\), and chaos erupts if \(x=2\)! Or does it...
Suppose we want to use circles to build a square by rolling a circle on a circle. Call the side of the target square \(s\) and the radius of our first approximation \(r_1\).
The first example inspired what has become Diverging Mathematics! It is a motivating topic for the Non-Euclidean Geometry seminar. Investigating surfaces that are piecewise flat is a powerful way to make this mysterious subject more accessible.
The second example leads to a very well-studied area of Calculus called MacLaurin Series, but it gets there in a surprising way that makes you Contemplate Infinity. Exposing students early to these fascinating series by building on their understanding of repeating decimals is an exciting way to revisit ideas, like addition, that seem very elementary ... but maybe not!
The last example is another excellent modern twist on an ancient idea. Ptolemy is often ridiculed for this idea of circles orbiting circle, but this example shows how surprisingly powerful this technique is!