Equations are just the boring part of mathematics. I attempt to see things in terms of geometry.
-Stephen Hawking
The most important observation we need to make is that geometry is an intrinsic property, meaning it is understood completely by exploring the space - no need to leave it and look back! Imagine that you are an ant crawling around on the surface of an infinite cone. You are so light and your feet are so sticky that you do not notice the effects of gravity.
- Can you tell if the surface is curved or flat?
- What about at the vertex?
Suppose you try to walk in a straight line along the surface of the cone. Observers would see you moving in an arc through space because they are looking from the outside, peering down on the cone. As far as you are concerned, you are walking in a perfectly straight line! These perspectives are shown in the image below. When the surface is viewed in 3D, it looks curved. If we cut along some seam, we can lay it flat.
Around the vertex, you notice some strange things. For instance, this straight line has intersected itself. That's new.
To work with these almost flat surfaces, we look for ways to lay a surface flat. This is exactly what happens when you draw a net.

If you were to print this out and fold along the dotted lines, the colored edges would coincide, and you would form a cube. Laid flat like this, you can imagine wandering around the cube: Each time you get to an edge, you come out on the other edge with that color!
Use this model to think about the following path:
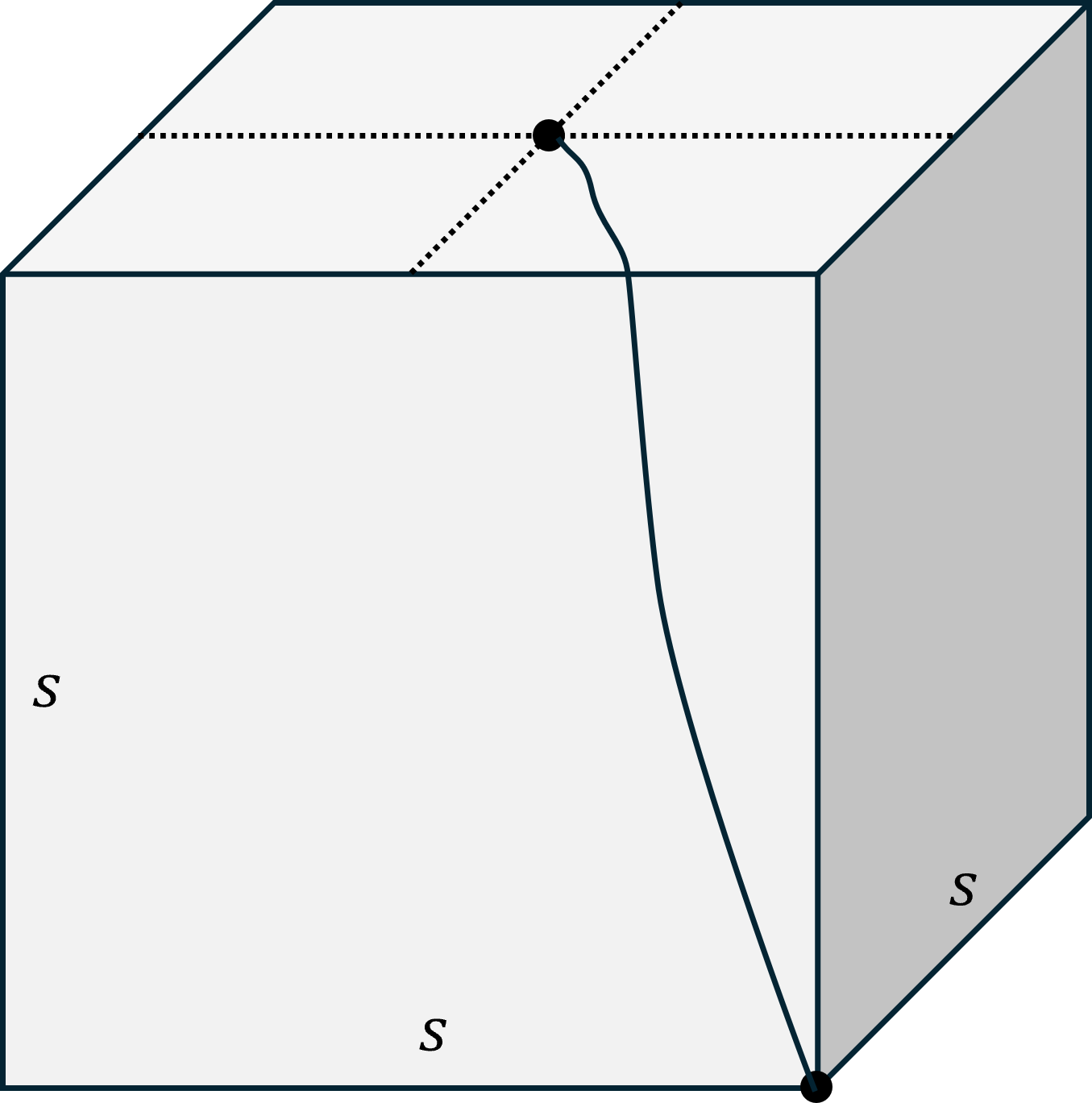
There are actually two paths (of equal length) connecting the center of the top face with the bottom corner. The other path is symmetric to the one shown, but part of it travels along the grey face.
A similar approach can be used to "unfold" the cylinder into two circular faces and a rectangle.
Consider two parallel lines on the circular face of a cylinder. Suppose each line bisects a radius and continues along the surface to the lateral side of the cylinder. What angle is formed when these lines intersect?

Any time something is made from flat materials, this
geometry describes the result.
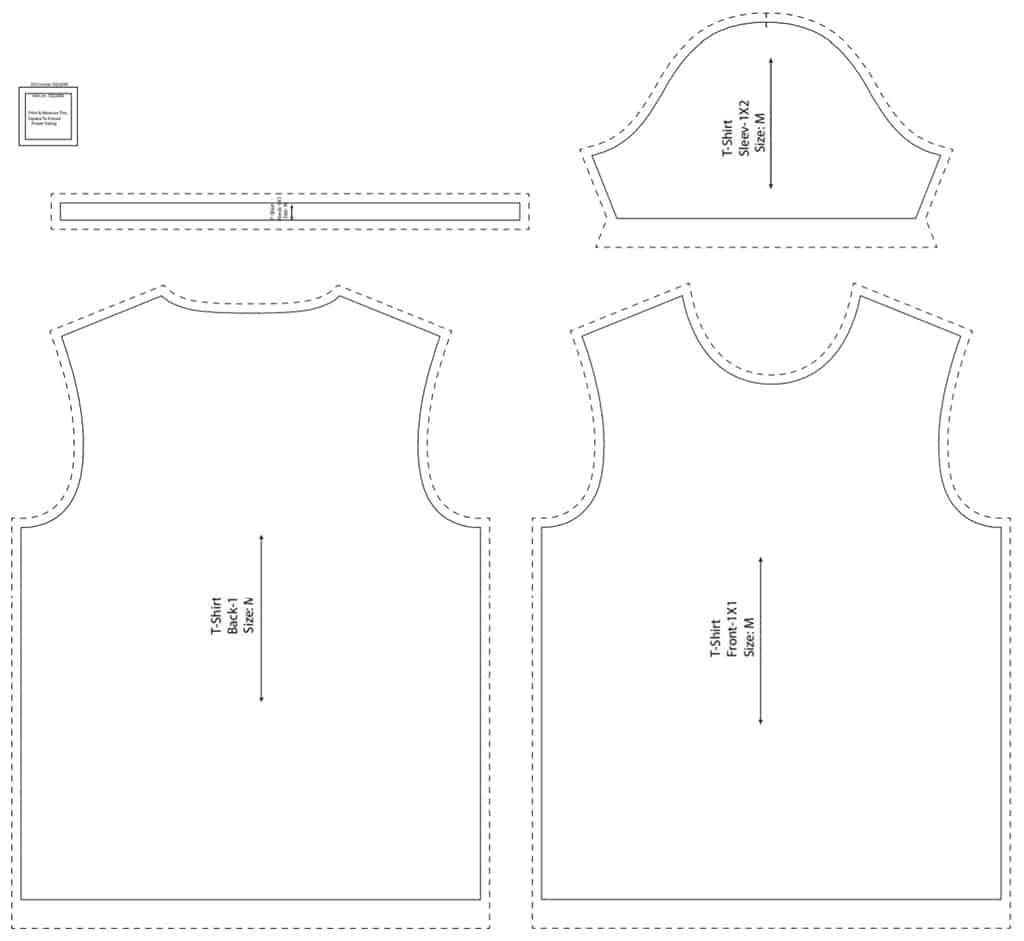
Clothing is made from flat textiles, but by sewing along seams, designers create shape. Even a simple T-shirt has a complicated template. Look at how the sleeves attach and compare them to some of your clothing.
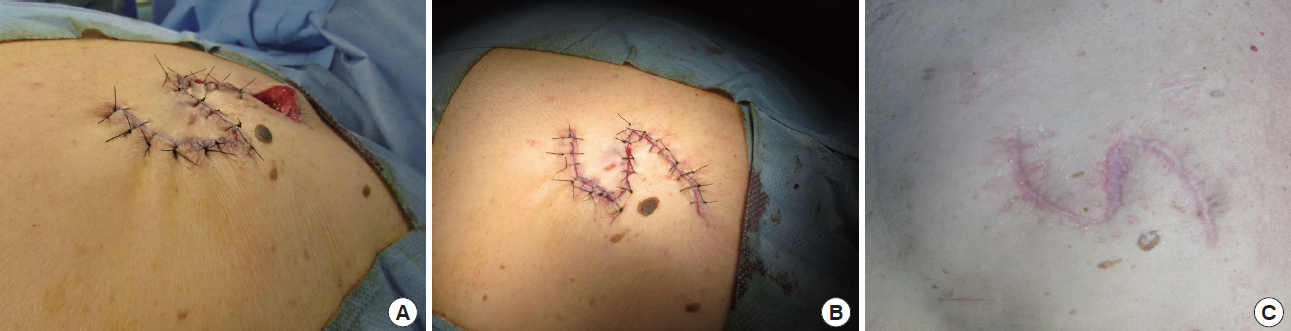
Surgeons slice into skin that lies flat, but when they are doing this to remove a tumor or patch of skin, they need to think about how to close the incision in a way that it heals flat. These images are from a 2015 paper.
Have you ever looked closely at the seams on new soccer balls? It makes you wonder how baseballs are made from two flat pieces of leather (???)!
