“Mathematics is not a careful march down a well-cleared highway, but a journey into a strange wilderness, where the explorers often get lost.” - William Sherron Anglin
A useful topic in Algebra is polynomial division. Consider the rational function \(f(x) = \frac{x^3+2x^2-5x -6 }{x -6}\). We start with how it is usually presented:
\[\begin{array}{r}
x^2-8x\phantom{,}+43\phantom{2,,6}\phantom{ab,}\\
x-6{\overline{\smash{\big)}\,x^3+2x^2-5x-6}}\phantom{ab,}\\
\underline{x^3-6x^2}\phantom{,-5x-6}\phantom{ab,}\\
8x^2-5x\phantom{2,,6}\phantom{ab,}\\
\underline{8x^2- 48x}\phantom{,,6}\phantom{ab,}\\
43x - 6\phantom{ab}\\
\underline{43x -259}\\
252
\end{array}\]
We then use this to rewrite the function:
\[f(x)= x^2-8x+43 + \frac{252 }{x -6}\]
This is useful to determine end-behavior, because if \(x\gg 0\) then the fraction at the end becomes very small. This is what it looks like graphically:
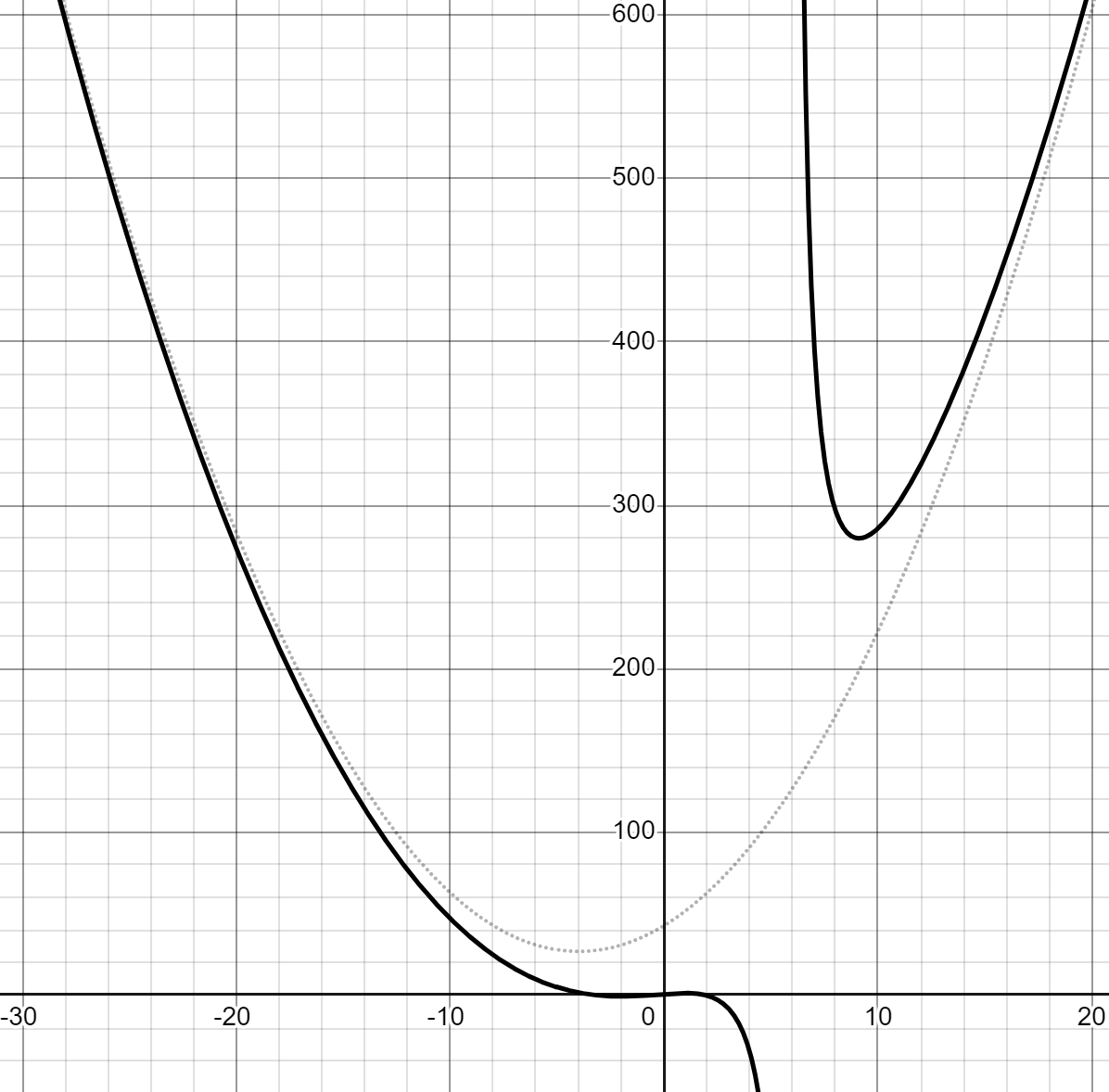
The result is that we "zoom out" and see the big picture. But what if we wanted to zoom in? Suppose \(x \approx 0\) - can you say anything about what this function looks like locally?
The division performed above orders the terms in decreasing size, so \(x^3\) came first, followed by \(x^2\) and so on. That's true if \(x\) is really big, but the opposite happens when \(x\) is very small. Try it and see what you get!
\[\begin{array}{r}
\phantom{ab}\\
-6+x{\overline{\smash{\big)}\,-6-5x+2x^2+x^3}}\\
\end{array}\]
There was once a topic covered in every high school class that taught students how to take square roots without a calculator. A decision was made at some point to cut this out because it was unlikely students would need it.
The algorithm looks a bit like the division algorithm, which means it might be possible to do something like the previous example did with polynomials.
Consider the function \(f(x) = \sqrt{4+x}\). What can we say if \(x\approx 0\)?
Note \(f(0)=2\), so we know that it crosses the \(y\)-axis at \(2\). We do not know the slope, but let's call it \(a_1\). For what value of \(a_1\) is \(\sqrt{4+x} \approx 2 + a_1 x\)? Remember that \(x\) is really small, so \(x^2\) is negligibly small.
Use Desmos to check your answer, and try to add on a quadratic correction. That is, consider \(2 + a_1 x+a_2 x^2\) and you can neglect terms like \(x^3\) and \(x^4\).
This is a very-labor intensive way to continue, so learning the "right" way to take square roots by hand may help.
This is a radical path that leads to such bizarre mathematics that it is considered a fringe topic. Nonetheless, it was studied by giants in 19th-century mathematics, and laid the groundwork which led to the discovery of catastrophic flaws in how we think about area and volume (See the Banach-Tarski Paradox, for example).
A nice overview of this topic is available on Wikipedia. Working through any of these examples will raise many more questions than it answers!