Mathematics is nourished by dreamers as it nourishes them. - John von Neumann
A beautiful consequence of the Inscribed Angle Theorem is that for a circle with a fixed diameter \(D\), the measure of an angle is uniquely determined by the length of the opposite chord. This can be used to prove the Law of Sines, but it actually shows something stronger (called the Extended Law of Sines):
\[\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = D\]
Ptolemy explored the natural case where \(D=1\), which is not the same unit circle we were all taught, but it has a similar effect, which normalizes things so that we can work directly with ratios. When inscribed in a unit diameter circle, the length of a side equals the sine of the opposite angle!
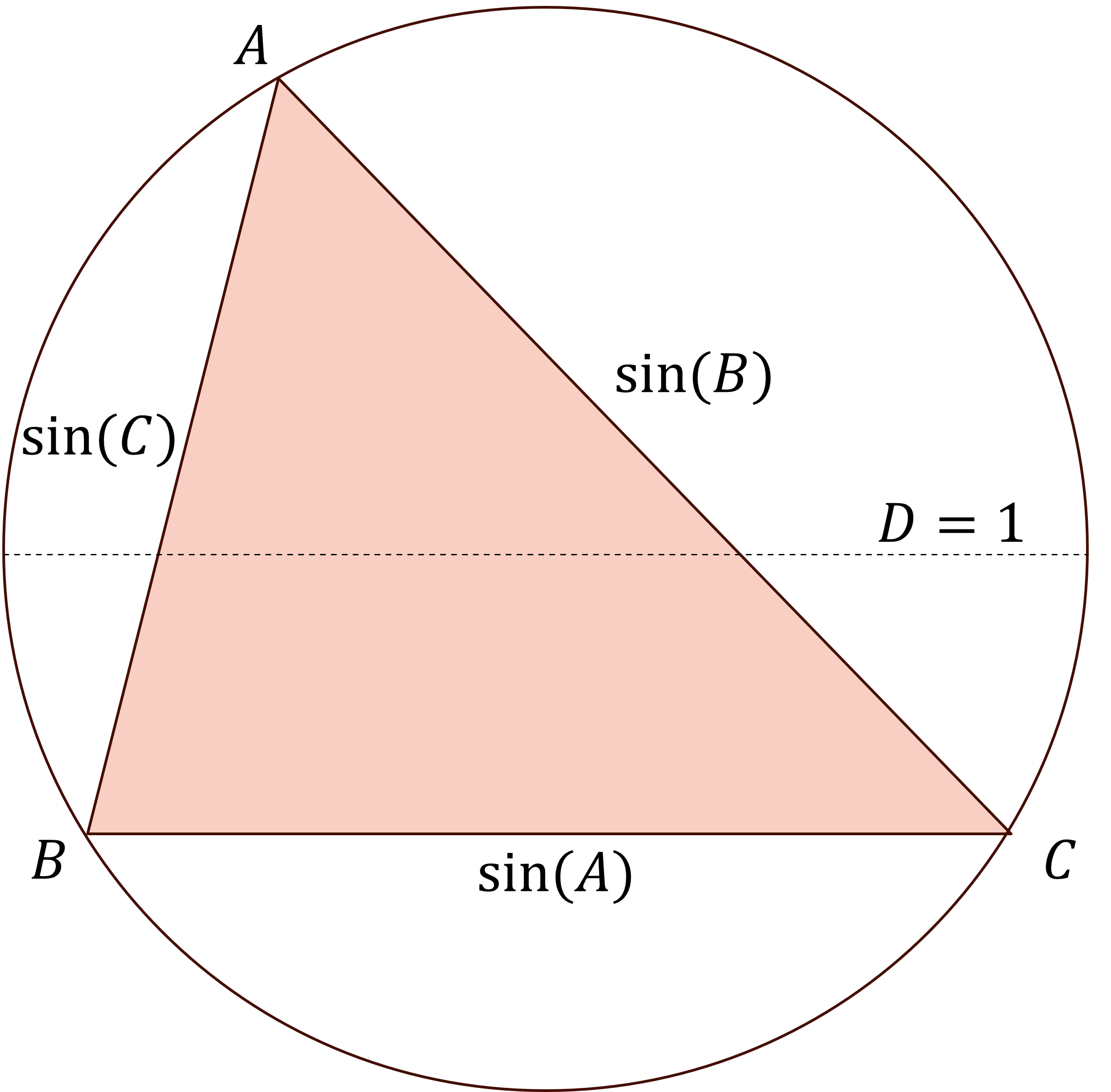
This picture already gives us three valuable insights about sine:
- The value of \(\sin 90^\circ\) is 1 because the opposite edge will be a diameter.
- For an angle of \(0^\circ\), the opposite chord is a point, so \(\sin 0^\circ=0\)
- There is symmetry around \(90^\circ\) because every chord (except the diameter) corresponds to both an acute and an obtuse angle.
This is only the beginning. For instance, it makes light work of the angle addition formula:
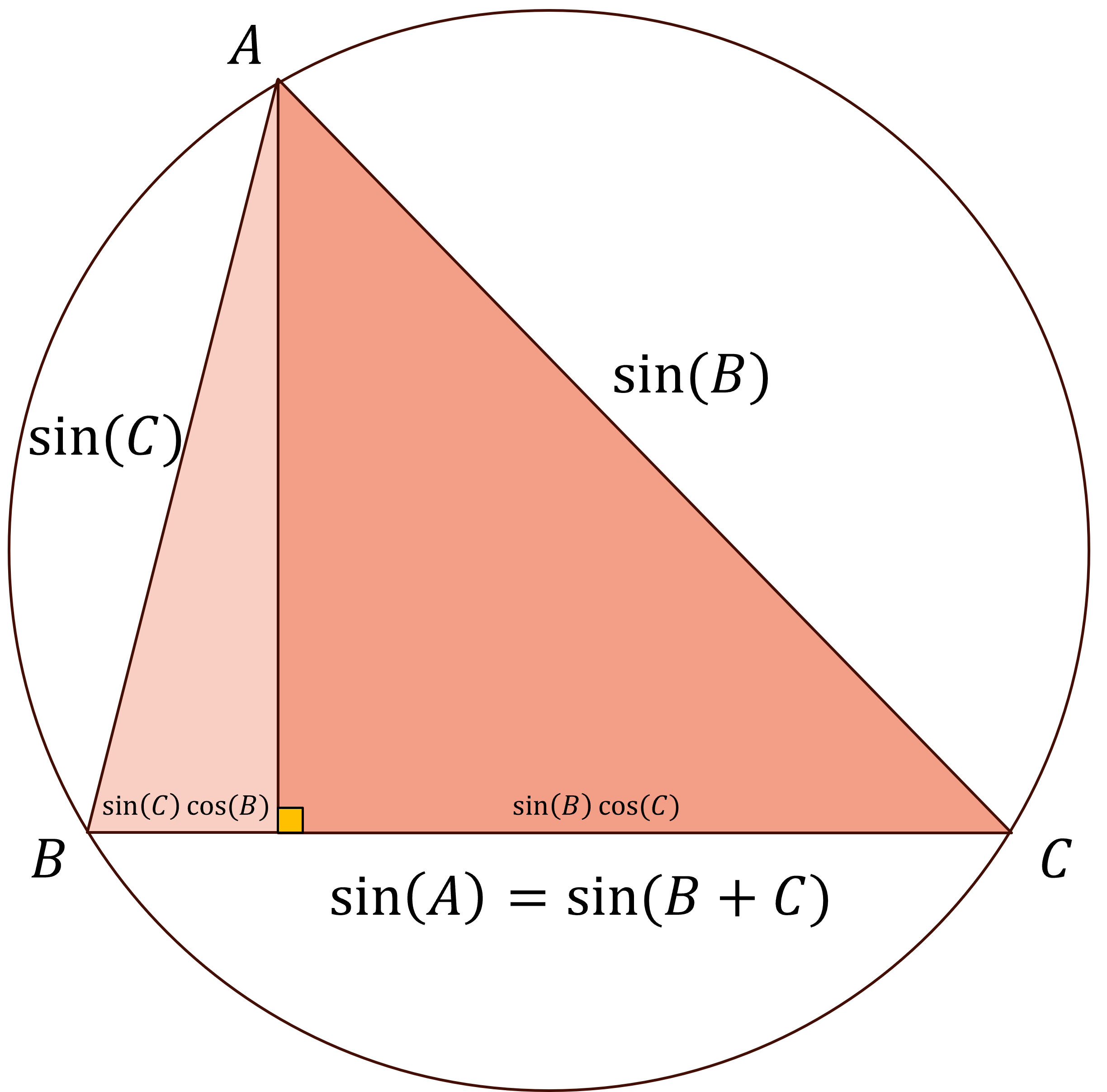
While the details of the historic record are interesting to read, our focus will be on the specific mathematical insights of Ptolemy's model. The challenge is to resolve the fact that the actual motion of the planets is elliptical, but we want to model this motion with circles. I have exaggerated the eccentricity of the ellipse in these drawings to emphasize the non-circularity.
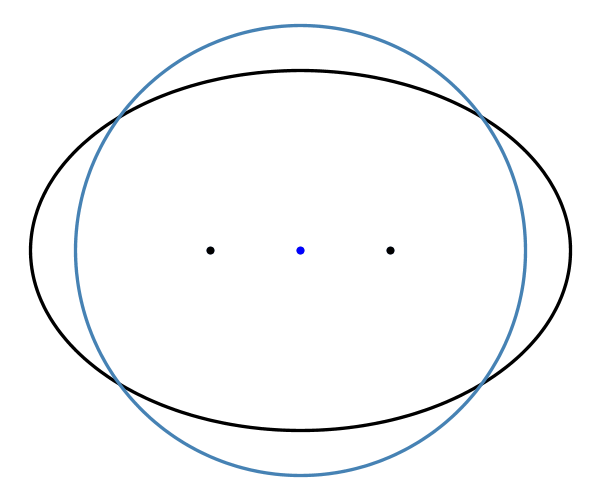
The first challenge for us mathematically is that the circle has a center, but the ellipse has two foci. Most people say Ptolemy's model puts the Earth at the center, but he scoots it off to the side a bit (so it is effectively at a focus!).
Next, we need to fix the different shapes. To do this, the sun will not travel along the circle itself, but rather it will orbit around a smaller circle whose center is also moving. So there are two things moving:
- The center of the smaller circle is moving at a constant speed
- The sun is moving around this smaller circle at a constant speed (and in the opposite direction?!).
This works perfectly:

This setup actually traces out the ellipse perfectly. The problem is not the shape of the orbit, but the time dependence. Ptolemy had ways to adjust for this, but the mathematics that led to thinking of an elliptical orbit as the composition of circular orbits is incredible. Fun Fact: These same circles can be interchanged without changing the resulting path!

There is nothing special about ellipses in Ptolemy's model: it can be used to trace any* orbit! I have collected a few here for your enjoyment, and encourage you to explore that asterisk.

